提要
观察法是通过直接观察发现规律,找到解决问题的一种常用方法。它是数学思维过程中必须掌握的一种方法,是类比,归纳的前提,是分析抽象的基础,是形成和发现数学知识的基本方法之一。正确灵活地使用观察法,可以避开常规解法中繁杂的运算,使解题过程简洁明快,给人耳目一新之感,且有助于创造性思维能力的培养。
知识全解
一.观察法的概念
观察是认识事物最基本的途径,是发现问题和解决问题的前提。解每一道数学题,都应先从观察入手,边看边想,从观察中找出特点,发现规律,从而使问题得以顺利解决,这是解决问题的最科学的方法,被形象地称为观察法。
二.数学解题中的观察途径
主要有3条途径:1.对数与式特征的观察;2.对图形结构特点的观察;3.对简单,特殊情况观察后的推广与归纳。
解决数学问题的观察法,是在掌握定理,法则,公式,图像等有关知识和经验的基础上,有意识,有目的地寻找对解题有帮助的规律和信息,观察法是解决问题的一种有效途径。
学法指导
类型1 求值
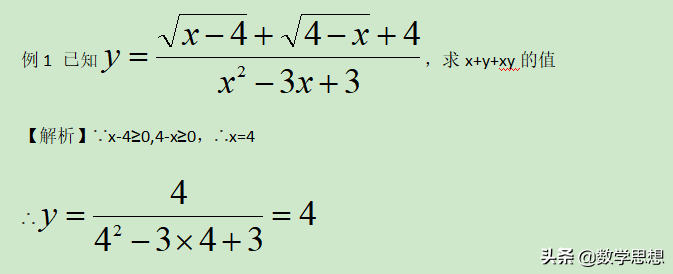
∴x+y+xy=4+4+4×4=24
【点评】本题看似难以下手,但只要细心观察,就不难从二次根式中发现x=4这一隐含条件。
类型2 探索规律
例2 观察下列算式:

链接中考
考点1 利用观察法解函数题
例1 如图所示,一次函数y1=x+b与一次函数y2=kx+4的图像交于点P(1,3),则关于x的不等式x+b>kx+4的解集是()
A. x>-2 B.x>0 C.x>1 D.x<1
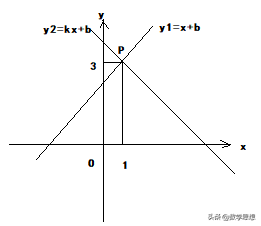
【解析】不等式x+b>kx+4的解集就是一次函数y1=x+b的图像在一次函数y2=kx+4上方时的x的范围,观察图像可知,当x>1时,一次函数y1=x+b的图像在上方。故选C
【点评】本题考查了一次函数和一元一次不等式的关系,解题时需要具有一定的观察能力,熟练掌握它们之间的关系是解题的关键。
考点2 利用观察法解变换题
例2 如图所示,在长方形ABCD中,AB=10,BC=5,点E,F分别在AB,CD上,将矩形ABCD沿EF折叠,使点A,D分别落在矩形ABCD外部的点A1,D1处,则阴影部分图形的周长为__
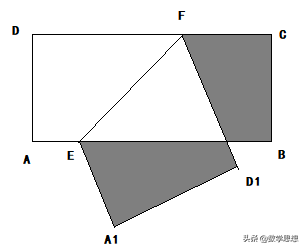
【解析】观察所给的图形,结合条件,不难发现阴影部分的周长为矩形ABCD的周长,所以阴影部分图形的周长=2(AB+BC)=2×(10+5)=30
【点评】本题若分别求出阴影部分的周长的各段线段的长再相加是不可能的,但利用观察法能使问题变得简单快捷。
考点3 利用观察法解探索规律题
例3 观察下列算式,你能发现什么规律?并用含n的代数式表示这个规律

【点评】解决此类问题的一般思路是:特殊→一般。